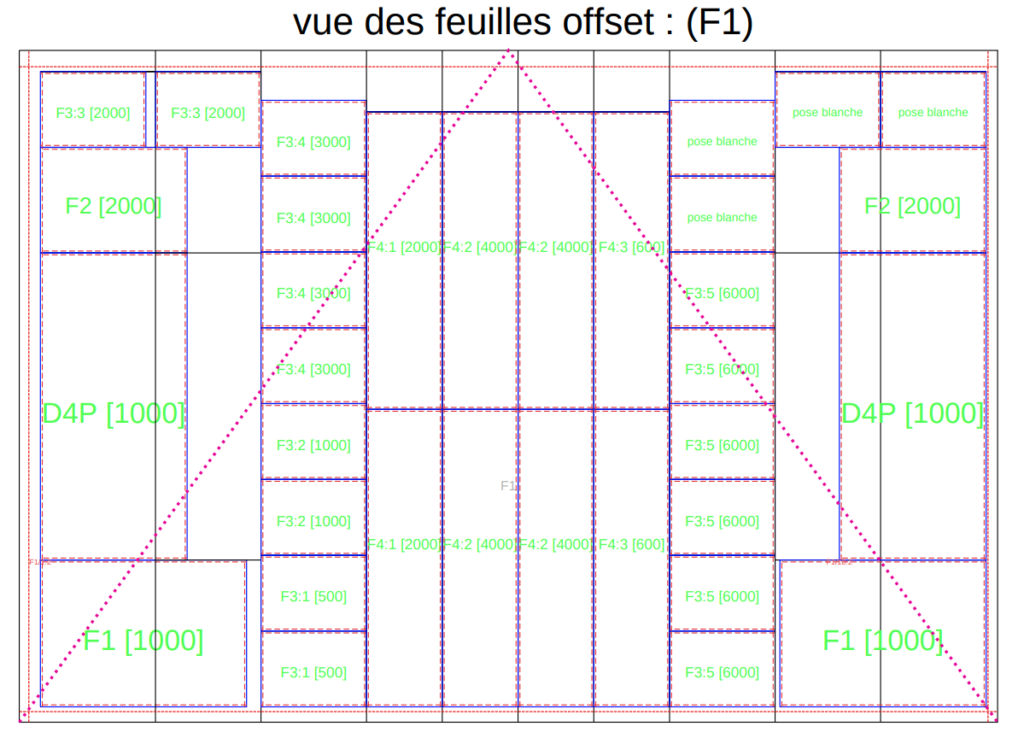
Objectif
Cette étude et réalisation permet de traiter efficacement le cas le plus général de l’amalgame de forme à imprimer sur une feuille d’impression, c’est à dire un ensemble de X formes multi-modèles de tirage différent en Offset feuille ou bobine sortie à plat :
Une forme Fx à plat est définie par une hauteur hx et une largeur lx.
A chaque forme Fx correspond un ensemble kx de modèles M de Q(M) produits.
{F1[M1-1/Q1-1 .. M1-k/Q1-k1] , F2[M2-1/Q2-1 .. M2-k2/Q2-k2] .. Fx[Mx-1/Qx-1 .. Mx-kx/Qx-kx]}
Le problème consiste à déterminer l’ensemble de feuilles d’impression minimisant le coût total de fabrication dans un référentiel de supports (papier, bobine, stock imprimeur, stock distributeur, fabrication) et un référentiel de poste de fabrication (presse offset feuille, rotative …).
{PF1(X1F1 .. X1Fx) .. PFz(XzF1 .. XzFx)}
Chaque feuille d’impression PF propose un vecteur de nombre de pose par forme.
Vf[X1F1 .. XxFx] puis par spécialisation de l’arrangement, un vecteur de nombre de pose par modèle Vm[X1M1 .. XxMw]. Avec comme ensemble de contraintes à satisfaire :
- Chaque modèle M apparaît sur une et une seule feuille PF.
- Pour chaque feuille d’impression PF, pour chaque modèle M, le nombre de bonnes feuille Qpf >= Qm / Xm ou Qm est la quantité objectif de modèle M et Xm le nombre de poses affectées au modèle M.
Méthodologie de résolution
Clariprint fait appel à plusieurs algorithmes d’optimisation, à travers les étapes suivantes :
A/ recherche de solutions de discrétisations du problème en classes de produit en explorant plusieurs quantités de classes (1 classe correspondant à 1 feuille d’impression au final). Clariprint utilise la méthode de discrétisation statistique de minimisation de l’inertie intra-classe. Le calcul de l’inertie utilise d’une part la surface des formes des produits, d’autre part les quantités objectifs pour chaque modèle de produit.
Clariprint utilise le solver de contrainte Choco pour minimiser la somme des inertie intra-classe avec un maximum pour la surface totale d’une classe.
B/ Pour chaque solution de discrétisation trouvée, pour chaque classe, génération de feuilles d’impression.
Clariprint fait appel à un problème Choco avec en entrée :
- liste des formes à imposer ;
- liste des quantités objectifs ;
- format maxi ;
Clariprint utilise 2 logiques de composition de feuilles d’impression différentes :
1/ N colonnes de forme unique + jusqu’à 2 colonnes de forme partagées (4 en bascule In8)
2/ N lignes de forme unique
Chaque logique est déclinée en 3 sous-logiques :
- côté-côté (pas de symétrie),
- In8 (symétrie d’axe parallèle à la hauteur),
- In12 (symétrie d’axe parallèle à la largeur)
Pour rappel les feuilles symétriques permettent de disposer sur un même côté de la feuille d’impression à la fois le Recto des produits et le Verso des produits, ainsi par basculement de la feuille avant un repassage, on peut imprimer à la fois le Recto et le Verso avec les mêmes plaques réduisant de moitié les coûts fixes d’impression par rapport à la méthode côté-côté.
C/ Les feuilles d’impression trouvées sont regroupées en vecteur de forme (nombre de pose pour chaque forme F1 .. Fx). Pour chaque discrétisation, pour chaque classe, Clariprint recherche le meilleur vecteur de forme (celui qui donne le tirage le plus faible). Clariprint utilise ici encore le solver de contraintes Choco.
D/ Enfin, pour déterminer la meilleure solution de fabrication, un algorithme de type Branch and bound explore les propositions de discrétisation dans les référentiels de ressources (papier, presse offset feuille, presse rotative …).